
- Geometric and arithmetic sequences worksheet how to#
- Geometric and arithmetic sequences worksheet series#
Therefore, a convergent geometric series 24 is an infinite geometric series where \(|r| < 1\) its sum can be calculated using the formula:īegin by identifying the repeating digits to the right of the decimal and rewrite it as a geometric progression. Sample problems are solved and practice problems are provided.\cdot1\) Arithmetic and geometric sequences worksheet ( with answer key + pdf) A sequence is an ordered list of items in mathematics (or events).
Geometric and arithmetic sequences worksheet how to#
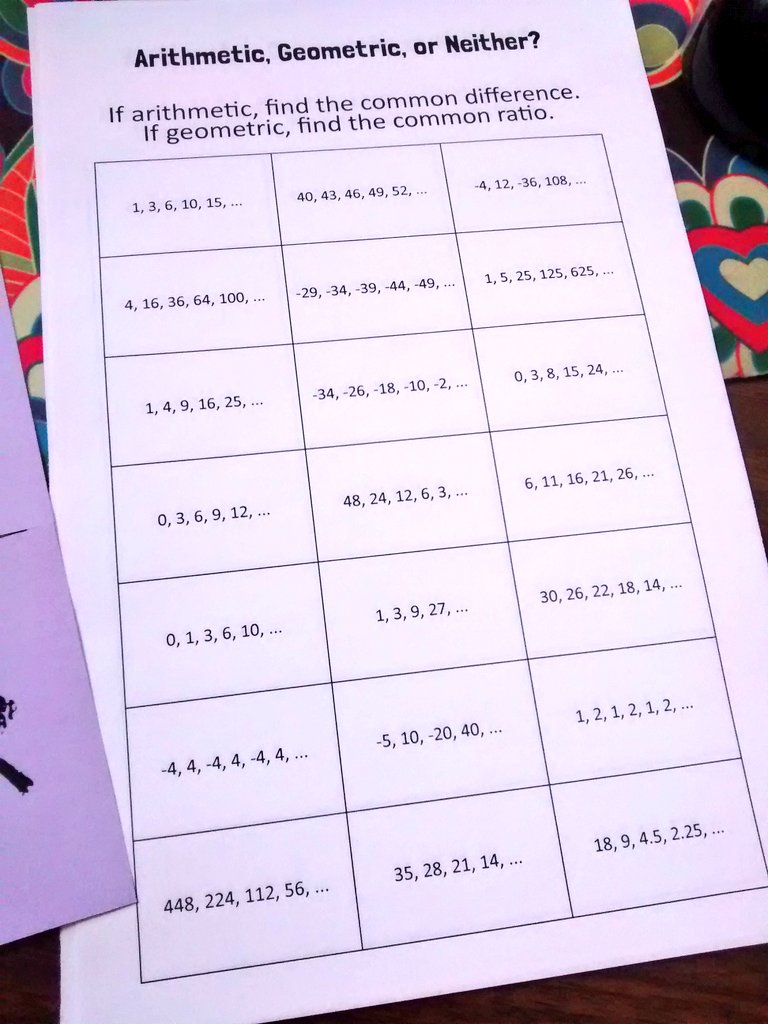
These worksheets explain how to use arithmetic and geometric sequences and series to solve problems. When finished with this set of worksheets, students will be able to recognize arithmetic and geometric sequences and calculate the common difference and common ratio. It also includes ample worksheets for students to practice independently. contain more Math Grade 6 Scope and Sequence 2021-2022 Mathematical Process Standards. This set of worksheets contains step-by-step solutions to sample problems, both simple and more complex problems, a review, and a quiz. TEKS Math Worksheets for ALL 6th Grade Math Standards:These 104. They will find the common ratio in geometric sequences. They will find the common difference in arithmetic sequences. This topic covers: - Recursive and explicit formulas for sequences - Arithmetic sequences - Geometric sequences - Sequences word problems. In these worksheets, students will determine if a series is arithmetic or geometric. These worksheets introduce the concepts of arithmetic and geometric series. The ratio, r, can be calculated by dividing any two consecutive terms in the sequence. Here, r is the common ratio between the consecutive terms. To find the next term in a geometric sequence, we use the following formula The common difference can be calculated by subtracting any two consecutive terms. Here, t_1 is the first term of the sequence, n is the term number that we need to find, and d is the common difference between two consecutive terms. To find the next term in an arithmetic sequence, we use the following formula In geometric sequence or series, there is a constant ratio being followed between consecutive terms. students will study pre-algebra topics, such as integer arithmetic. The first difference is that the arithmetic sequence follows a constant difference between consecutive terms. The worksheets are randomly generated each time you click on. So, what is the difference between these two basic types of sequences and series? The most basic ones are arithmetic and geometric. There are a variety of different types of these sequences and series. The series, on the other hand, is a process of adding infinitely many numbers without a fixed order. When talking about sequence and series in mathematics, a sequence is a collection of numbers that are placed, following a specific order with repetitions allowed. Observe the sequence and use the formula to obtain the general term in part B. Use the general term to find the arithmetic sequence in Part A. Series, on the other hand, is the arrangement of similar things one after the other, without following a fixed order. This set of worksheets lets 8th grade and high school students to write variable expression for a given sequence and vice versa. By sequence, we mean a list of things that obey a specific order. We come across the terms 'sequence' and 'series' very often in our lives. A geometric sequence is a sequence of numbers in which after the first term, consecutive ones are derived from multiplying the term before by a fixed, non-zero number called the common ratio. An arithmetic sequence is a sequence of numbers in which the interval between the consecutive terms is constant.


 0 kommentar(er)
0 kommentar(er)
